文章背景
本文介绍了一个通用的用于求解VRP问题的元启发式邻域搜索框架,本框架也是 Vidal在其extend neighborhood中使用到的搜索框架, 整篇文章的思想比较简单,主要从以下三个方面来对问题建模:
- 如何设计一种简单的元启发式搜索框架
- 如何实现giant tour solution与VRP solution之间的编码解码转换
- 如何利用sequential search的方法来加速领域搜索过程
启发式 VS 元启发式
早期VRP问题多使用启发式算法来进行求解,目前启发式算法主要用于
元启发式算法的解初始化,有代表性的方法有1
- merge heuristic
- saving-based heuristic
- two-phase methods
- cluster-first route-second
- route-first cluster-second
元启发式算法目前是主流,因为具有问题不相关性,可以作为一个抽象框架
与其他搜索技术进行集成,Coedeau2发现目前种群类的元启发式算法表现
要好于禁忌类搜索算法
算法思想
| 算法术语 | 说明 |
|---|---|
| $S$,$S^*$ | 解, 已知最优解 |
| $f(S)$,$f(S^*)$ | 解目标函数,已知最优解函数 |
| $H$ | 确定性贪心启发式搜索算法 |
| $HR$ | 随机贪心启发式搜索算法 |
| $Mutate$ | 解扰动过程 |
| $np$ | 解初始化搜索次数 |
| $ni$ | 解邻域搜索次数 |
| $nc$ | 每轮搜索生成的子代解个数 |
1.1 GRASP
(GRASP)主要思想就是对搜索起点进行随机初始化。
该方法需要与其他搜索算法结合才会有比较好的表现

$np=1$, $ni>1$, $nc=1$
1.2 ILS

$np=1$, $ni>1$, $nc=1$
在每轮local search之前,要进行mutate的操作来使搜索空间跳出当前局部最优空间
跳出的太大没有连续性;跳出的太小,无法跳出当前局部最优点
1.3 ELS
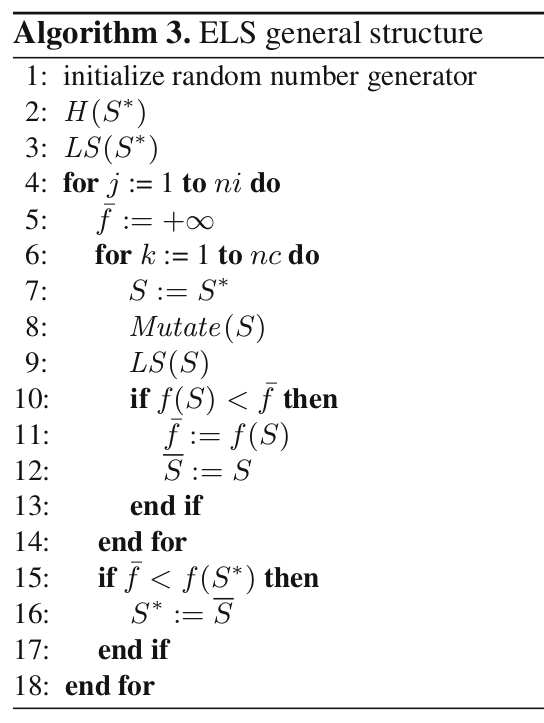
$np=1$, $ni>1$, $nc>1$
ELS的本质想法就是在ILS的基础上,通过mutate的操作增加对当前解邻域空间的采样
1.4 混合搜索
GRASP可以与ILS以及ELS算法很好地结合,想法也很简单

local search在vrp问题上的应用
本文提出的ILS方法使用了giant tour mutation与vrp solution local search
相结合的方法。通过在giant tour上搜索,进而通过split算法将对giant tour
进行decoding, 从而获得对应最优解。这种方法的好处在与可以在不损失解信息
的情况下,使用求解TSP的算法,降低搜索难度。
TSP问题的最优解并不一定是VRP问题的最优解,这里会存在discrepancy,这也是这种方法的一个弱点

在具体的move操作上,文章使用了sequential search的方法来加速搜索,

RNNH表示Randomized Nearest Neighbor Heuristics