文章背景
CARP问题与CVRP问题的区别
- CVRP
- 可以看做traveling salesman problem(TSP)的拓展,TSP问题属于NP-hard问题
- 每个任务的服务方式是唯一的
- 不同任务之间的距离信息是固定的
- CARP
- 可以看做Chinese postman problem(CPP)的扩展,CPP问题目前存在多项式复杂度的求解算法
- 每个任务至少有两种服务方式,比如一条边任务可以从两个方向服务
- 不同任务之间的距离信息不是固定的,随着服务方式的变化而变化
相比于CVRP任务,CARP任务的难点在于每个任务有多个服务方式,使用不同的服务方式又会导致不同的服务成本。
文章思想
将CARP的解空间分解为四个子空间
- Assignment: 每条路径所服务的任务
- Sequencing: 任务的服务顺序
- Mode Choice: 每个任务的服务顺序
- Paths: 相邻任务之间的空载路径
这四个子空间之间存在依赖关系,通过在其中的一个子空间内进行搜索,其他子空间内的信息可以 在多项式复杂度的时间内推导出。这种方式的关键在于如何减少在推导过程中的计算复杂度。
| 子空间信息转化 | 求解算法 |
|---|---|
| 2->1 | tour spliting算法 $O(n^{2})$1, $O(n)$2 |
| 2->4 | Dijkstra算法 |
| 2->3 | dynamic programming $O(n)$3, $O(1)$4 |
本文的主要贡献是在2->3的部分进行了优化
算法核心
问题定义
已知一组任务序列$\sigma = (\sigma (1)…\sigma(\left | \sigma \right |))$ 每一个任务$i$存在有限个服务模式$M_{i}$,需要找到一组最优服务模式组合,使得总服务成本最小
之前怎么做
构建辅助图$H_{\sigma}=(V_{\sigma},A_{\sigma})$ 总共包含$\sum_{i=1}^{|\sigma|}|M_{\sigma(i)}|$ 点的数量, 每一个点对应每一个任务的一种服务方式,任意两个连续服务对之间连接一条边,边的成本为$ c_{\sigma(i)\sigma(i+1)}^{kl}+s_{\sigma(i)}^{k}$, 其中第一项表示以模式$k$服务任务$i$,以模式$l$服务任务$i+1$所对应的遍历成本,第二项表示以模式$k$服务任务$i$所对应的服务成本
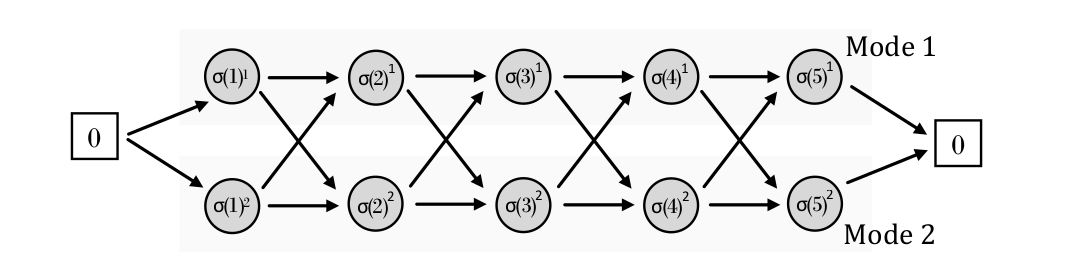
这种图属于有向无环图,存在拓扑排序,利用Bellman算法可以在$O(n)$复杂度内求解
动态规划:用空间换时间
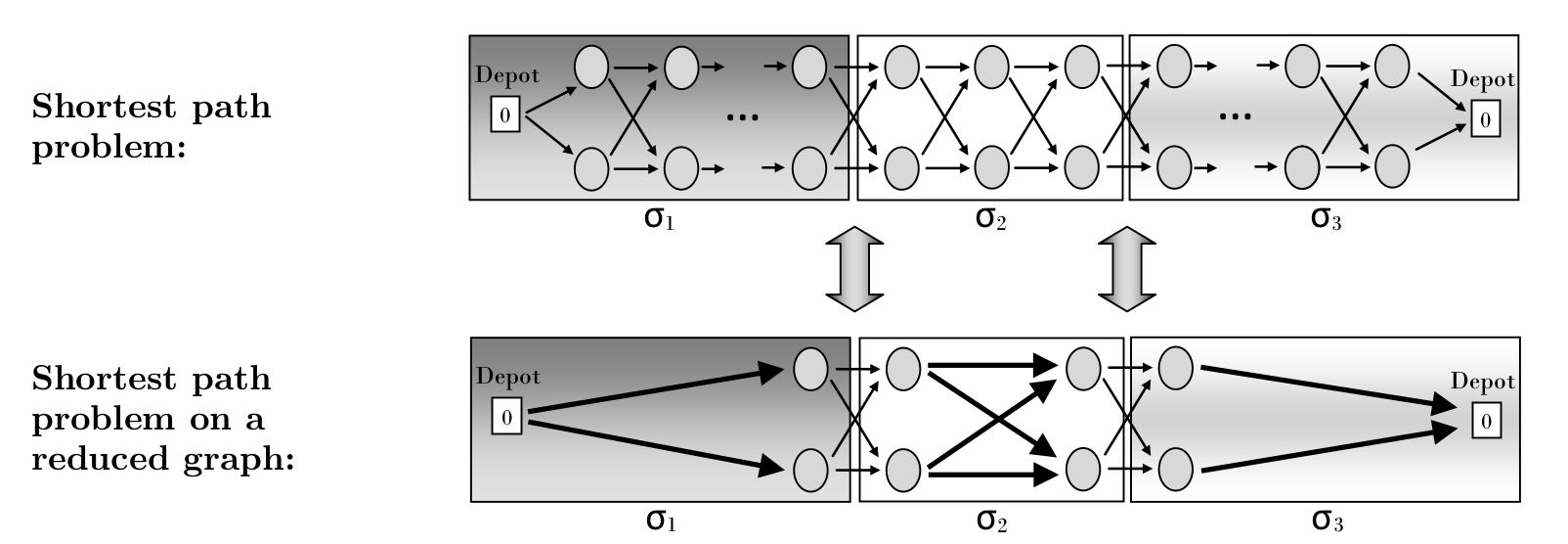
在之前的方法中,当每一次move发生后,需要重新从0开始构建新辅助图的最短路径信息。但我们可以看到, 在local search中的move都属于局部扰动,图中的信息很多都没有变化,如果可以利用某种子结构来维护 这类信息,那么可以大幅降低问题的求解时间。
作者定义了子问题结构$C(\bar{\sigma})[k,l]$,该结构表示对于任意一个子路径,当第一个任务以模式$k$服务, 最后一个任务以模式$l$服务,所对应的最短路径。从几何角度来讲,就是上图中任意两个节点之间的最短路径。 基于该结构,我们可以得出相应的递推公式: \[C(\sigma_{1} \oplus \sigma_{2})[k,l]=\underset{x\in M_{\sigma1(|\sigma1|)}}{\min} \left \{ \underset{y \in M_{\sigma2(1)}}{\min} \left \{ C(\sigma_{1})[k,x]+c_{\sigma1(|\sigma1|)\sigma2(1)}^{xy}+C(\sigma2)[y,l] \right \} \right \} \tag{1} \label{1}\]
对于只包含一个任务的子序列(也就是base case),我们有如下定义: \[C(\bar{\sigma})[k,l] = \left\{\begin{matrix} s_{i}^{k}, &&& k = l \\ +\infty, &&& otherwise \end{matrix}\right.\]
其中$\oplus$表示对两个子序列的拼接,在具体的计算过程如下:
- 基于当前解,会首先计算所有子序列的最短路径,该计算的时间复杂度为$O(n^{2})$
- 利用\eqref{1}式得到的子结构,来对move操作后得到的新解进行evaluation,因为只需要对 move操作修改的地方进行局部更新,这里的复杂度为$O(1)$
进一步剪枝,提高搜索效率
大量的move evaluation并不会带来解的提升,即使将move操作限制在相邻任务上5,作者在实验中发现, 如果在move搜索过程中将进行预剪枝操作,
可以减少大约90%的无谓move操作。
具体的想法很直觉
首先,我们定义一个move作用于两个路径$\sigma1,\sigma2$,产生两条新的路径${\sigma_{1}}’,{\sigma_{2}}’$
任何一个move如果能带来解的提升,那么需要满足如下式子
\[\Delta_{\Pi}^{LB}=C({\sigma_{1}}')+C({\sigma_{2}}')-C(\sigma_{1})-C(\sigma_{1})<0 \tag{2}\]
我们设$C_{LB}({\sigma}’)$为路径${\sigma}’$的成本下界,即$C_{LB}({\sigma}’)\leqslant C({\sigma}’)$,所以有
\[\color{Orange}{C_{LB}({\sigma_{1}}')+C_{LB}({\sigma_{2}}')-C(\sigma_{1})-C(\sigma_{1})\leqslant
C({\sigma_{1}}')+C({\sigma_{2}}')-C(\sigma_{1})-C(\sigma_{1})}\]
所以可以使用$C_{LB}({\sigma_{1}}’)+C_{LB}({\sigma_{2}}’)-C(\sigma_{1})-C(\sigma_{1})<0$
来作为预判断进行剪枝
给定一个路径$\sigma_{1}$, 我们定义其下界为 \[\begin{eqnarray*} C_{LB}(\sigma_{1} \oplus ... \oplus \sigma_{K})&=&\sum_{j=1}^{K}C_{MIN}(\sigma _{j}) +\sum_{j=1}^{K-1}c_{\sigma_{j}(|\sigma_{j}|)\sigma_{j+1}(1)}^{MIN} \tag{3.1}\label{3.1} \\ C_{MIN}(\sigma)&=&\min_{k \in M_{\sigma(1)}}\left \{ \min_{l \in M_{\sigma(|\sigma|)}}\left \{ C(\sigma)[k,l] \right \} \right \} \tag{3.2} \\ c_{ij}^{MIN}&=&\min_{k \in M_{i}}\left \{ \min_{l \in M_{j}}\left \{ c_{ij}^{kl} \right \} \right \} \tag{3.3} \end{eqnarray*}\]
\eqref{3.1}可以在$O(1)$的复杂度内完成evaluation。
1. move evaluation技术的应用
1.1 与现有搜索算法集成
1.1.1 local search + move evaluation
可以看到当前的move evaluation技术是在move的粒度上进行加速优化的,所以可以作为building block来集成进当前的 搜索算法,文章中作者尝试将move evaluation集成进local search算法67
 move evaluation.png)
1.1.2 预处理阶段的计算长度优化
对于长路径序列,如果在预处理阶段计算所有的子结构,其实会有大量冗余,比如 \[\sigma (1,10)=\sigma (1,3)\oplus \sigma(4,10)=...=\sigma (1,8)\oplus \sigma(9,10)\]
Irnich8提出限制预计算子序列个数为$O(n^{\frac{4}{3}})$或$O(n^{\frac{8}{7}})$,$n$为序列长度。 本文作者选择了一个更简单的策略来实现预计算精简:
- 计算第一个任务为仓库的子序列
- 计算最后一个任务为仓库的子序列
- 计算任务个数不超过10个的子序列
1.2与复杂搜索move集成
1.2.1 Polynomial ejection chains
ejection chains9 是通过一系列相互依赖的连续move操作实现的解提升搜索算法,其搜索过程如下:

同样这个问题也属于基于辅助图构建最短路径,当基于辅助图发生move局部扰动后,我们同样可以使用本文的动态规划技术来 计算出扰动后新图的最短路径。
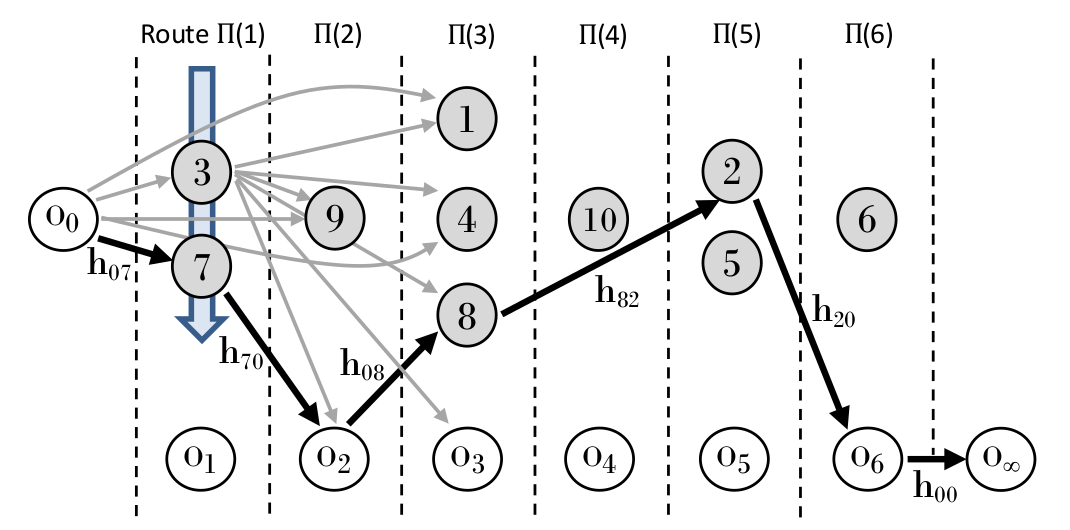
上图表示了一个包含10个任务,6条路径的问题解,其中最短路径由黑色实心箭头标出,表示将7号任务从路径R1移至 R2,8号任务从路径R3移至R5,2号任务从路径R5移至路径R6,可以产生一个成本更低的解。
1.3 对含多服务模式的路径规划问题建模
因为move evaluation可以很好地解决一个任务有多个服务模式的问题,所以我们可以对类似的问题都使用move evaluation 来加速搜索。
1.3.1 混合车辆路径问题
- 点任务 $|M_{i}| = 1$
- 弧任务 $|M_{i}| = 1$
- 边任务 $|M_{i}| = 2$
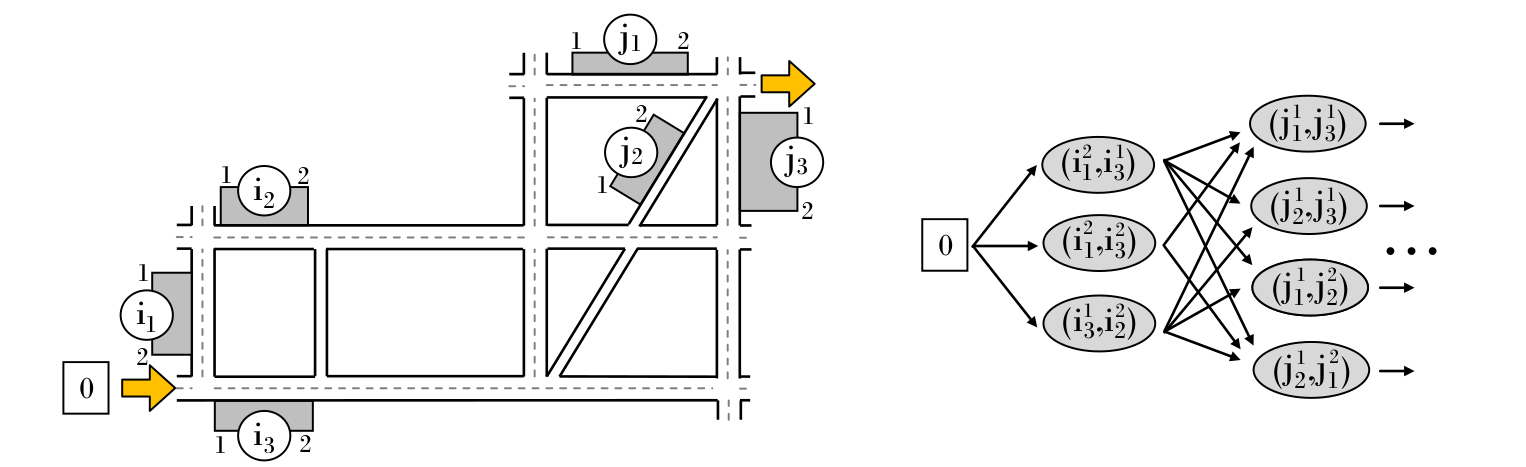
1.3.2 在复杂路口处有延迟与转向约束问题
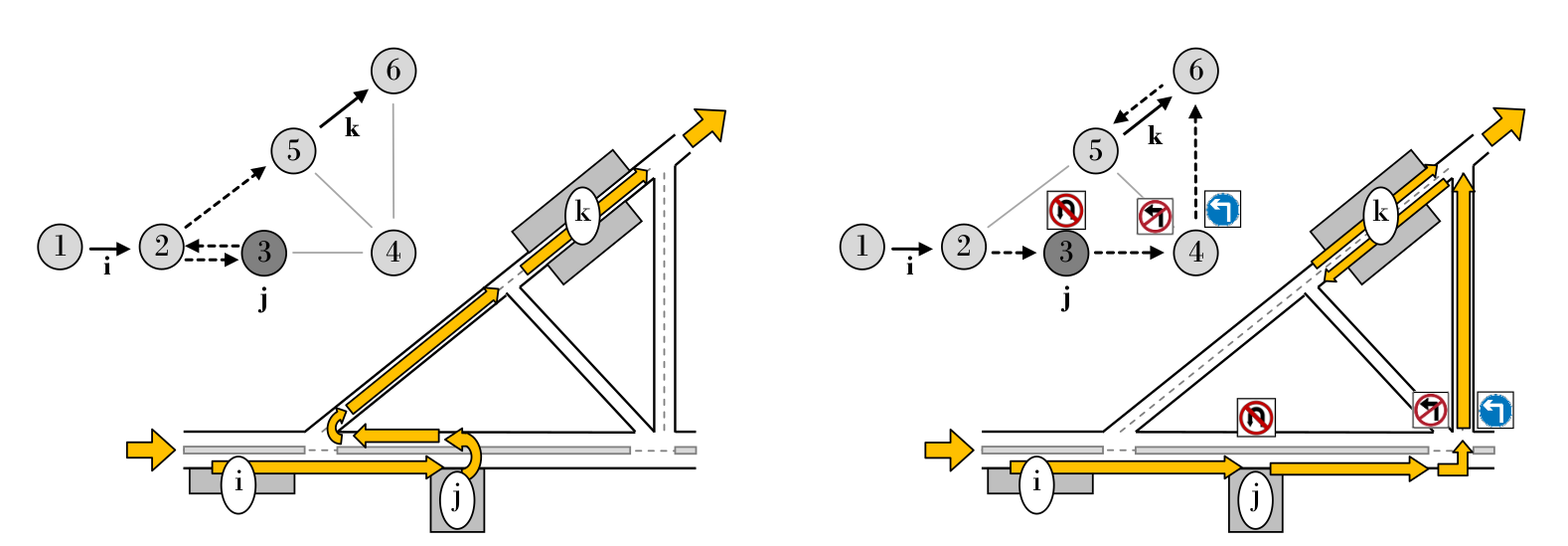
- 点任务 $|M_{i}| = p_{i}$, $p_{i}$表示每个点任务的入度,不同的入度表示不同的服务方向
- 弧任务 $|M_{i}| = 1$
- 边任务 $|M_{i}| = 2$
1.3.3 服务聚类问题
对于服务聚类问题,将服务按组分割,每个组内的任务需要被连续的服务,如果我们可以将每个组抽象为一个任务, 组内任务的不同服务方式对应抽象任务的不同服务模式,那么我们同样可以使用move evaluation技术来加速搜索。
1.3.4 其他的问题
move evaluation技术的关键在于可以对具有多服务模式属性的问题进行优化加速,所以对于任意的车辆路径规划问题, 只要其可以建模为类似的多服务模式问题,那么就可以使用该技术来提高搜索效率。
- generalized VRP问题,每一个任务有多个可服务位置,必须选择其中一个位置进行服务,如果将每个任务的服务位置
建模为任务的一种服务模式,那么就可以自然地使用move evaluation技术。
- 只要一个任务的服务可以被建模为多种不同服务模式,包括但不限于是否加油,行驶速度,是否经过某些服务设施等等。 这些问题涉及多类资源约束问题,属于resource constrained shortest path subproblems(RCSPP)。
实验分析
本文将move evaluation技术集成进了两种元启发式搜索算法 ILS, UHGS,具体实现细节可以参考相关文章
参数配置
| ILS超参 | 参数大小 |
|---|---|
| giant tour 扰动次数 $k$ | $k=2+\lfloor n/200 \rfloor$ |
| 未提升搜索次数 $n_{I}$ | $n_{I}=100$ |
| 每轮子代解生成个数 $n_{C}$ | $n_{C}=50$ |
| 搜索启动次数 $n_{P}$ | $n_{P}=5$ |
| 单轮搜索最长时间 $T_{MAX}$ | $T_{MAX}=1h$ |
| UHGS超参 | 参数大小 |
|---|---|
| $\mu^{MIN}$ | $\mu^{MIN}=25$ |
| $\mu^{EL}$ | $\mu^{EL}=12$ |
| $\mu^{GEN}$ | $\mu^{GEN}=40$ |
| $I_{MAX}$ | $I_{MAX}=20,000$ |
| $T_{MAX}$ | $T_{MAX}=1h$ |
算例信息
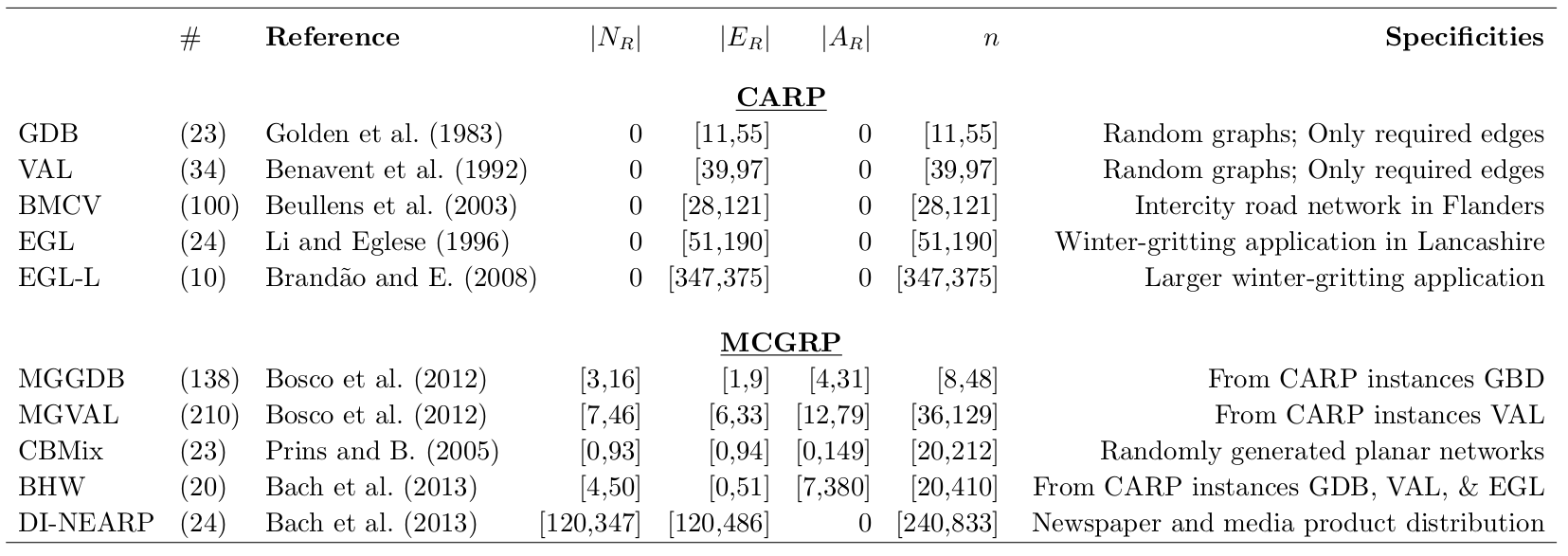
评价指标
- 与最优解的差距(average/best percentage gap): $\frac{100(z-z_{BKS})}{z_{BKS}}$
- 求解时间$T$
- 最优解求解时间$T^{*}$
结果分析
- 在使用了move evaluation技术后,ILS与UHGS相比于之前的方法都有显著提升,在大规模算例上,
UHGS的表现要优于ILS。
- 作者利用reduction的方法将CARP问题转化为了CVRP问题用未使用move evaluation的技术求解,结果显示算法 效果要差于使用move evaluation的方法。
下一步方向
- 目前在车辆路径规划问题上,主流从两个level来研究,第一个方向是本文的low-level小粒度搜索结构优化, 第二个研究方向是high-level搜索框架优化10,同时可以探索今后两类方法的高效结合。
- 研究多资源约束的车辆路径规划问题,构建相应的扩展领域结构。
- 进一步探索问题的领域结构,提高local search的搜索效率。
-
Tour spliting algorithms for vehicle routing problems. C. PRINS et al. ↩
-
Technical Note: Split algorithm in O(n) for the capacited vehicle routing problem. Thibaut Vidal. ↩
-
A guided local search heuristic for the capacitated arc routing problem. Beullens et al. ↩
-
Node,Edge, Arc Routing and Turn Penalities: Multiple problems - One Neighborhood Extension. Thibaut Vidal. ↩
-
The granular tabu search and its application to the vehicle-routing problem. Toth.P, D.Vigo. ↩
-
A unified solution framwork for multi-attribute vehicle routing problems. Vidal, T. et al. ↩
-
The granular tabu search and its application to the vehicle-routing problem. Toth.P, D.Vigo. ↩
-
A unified modeling and solution framework for vehicle routing and local search-based metaheuristics. Irnich, S. ↩
-
Ejection chain and filter-and-fan methos in combinatorial optimization. Glover, F., Rego. ↩
-
A hibrid metaheuristic approach for the capacited arc routing problem. Chen, Y. et al. ↩