1. 文章总览
本文是第一篇将MCGRP问题与时间窗问题统一建模的文章,作者通过将原问题 转化为在有向图上的VRPTW问题,之后使用了Branch-price-and-cut方法来求解。
2. 问题建模
2.1 原问题建模
给定$G(V,A,E)$
- $V=\{0,1,2,…,n\}$表示点集,$0$为仓库点,$V_R \cup V_{NR} = V$
- $V_R$表示有需求的点
- $V_{NR}$表示没有需求的点
- $A=\{(i,j) \subseteq V \times V \}$表示弧集合,$A_R \cup A_{NR} = A$
- $A_R$表示有需求的弧
- $A_{NR}$表示没有需求的弧
- $E=\{(i,j) \subseteq V \times V : i < j\}$表示边集合,$E_R \cup E_{NR} = E$
- $E_R$表示有需求的弧
- $E_{NR}$表示没有需求的弧
为简便起见,我们使用$link(i,j)$表示图中的连接元素,即$link = E \cup A$, 对每一条link,我们有两类特征
- 成本特征, 遍历成本$c_{i,j}$
- 时间特征,遍历时间$t_{i,j}$, 服务时间$s_{i,j}$
对于每一个任务,我们有两个特征
- 需求$d_{i,j}$
- 时间窗$[a_{i,j},b_{i,j}]$,必须要在该时间窗内抵达该任务
假设我们有一个路径序列$[0,w_1,…w_n,0], w_{i} \in V_R \cup A_R \cup E_R$, 我们定义,
- 累计载重$cumd(k):\sum_{i=1}^{|w|-1}d_i \leqslant Q$
- 抵达时间$cumt(k):a_{w_k(i,j)} \leqslant \sum_{u=1}^{k-1}s_{w_u(i,j)}+\sum_{u=0}^{k-1}t_{w_{u,1}{w_{u+1,0}}} \leqslant b_{w_k(i,j)}$
2.2 问题转化
可以看到原问题在服务类别与服务约束上都有比较复杂,为此,考虑将问题进行转化,等价的建模为传统的VRPTW问题 基本思路就是将不同的服务类型抽象为节点,同时要保证对这些节点的有序访问等价于原问题的服务顺序。 为此,文中借鉴Baldacci, R. et al1的想法,进行问题的转化
$G(V,A,E) \Rightarrow \hat{G}(\hat{V},\hat{A})$,其中$V_R,A_R$对应一个点, $E_R$对应两个点,仓库点对应两个点$0_1,0_2$,其中$0_1$入度为$0$, $0_2$出度为$0$, $\hat{A}$保证了图的连通性。对于边任务$(i_1,i_2)$,我们使用两个点来表示,$i=i_1,i_2$; $i^{\prime}=i_2,i_1$, 因此$|\hat{V}|=|V_R|+|A_R|+2|E_R|+2$,因为我们将一个边任务分为了两个点, 所以我们要将边任务的相关服务特征信息平分在两个点上
- $\hat{d_i}=\hat{d_{i^{\prime}}}=\frac{1}{2}d_{i1,i2}$
- $\hat{s_i}=\hat{s_{i^{\prime}}}=\frac{1}{2}s_{i1,i2}$
2.2.1 cost的转化建模
一个trivial的弧构造方法就是在完全图的基础上删去不满足载重约束与时间窗约束的弧

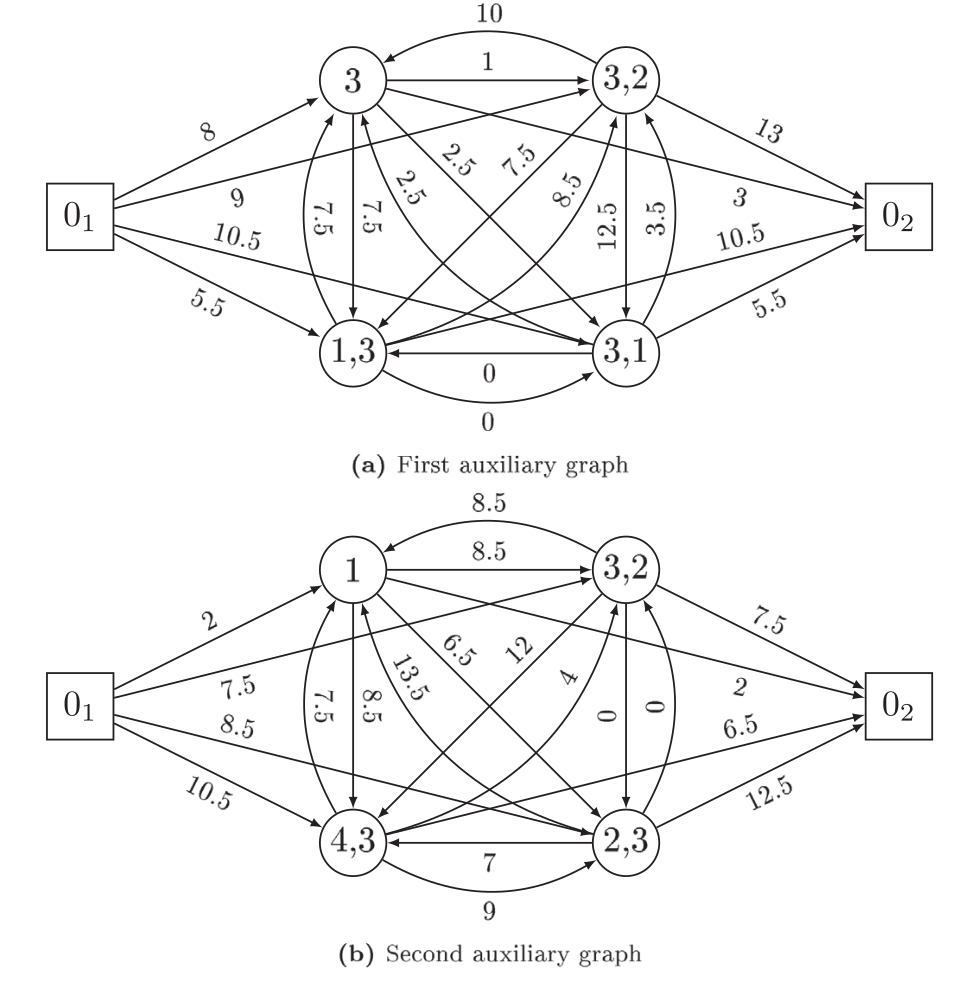
原问题中的每一条路径(route)对应辅助图中的一条从$0_1 \rightarrow 0_2$的路径(path)
原问题中如果服务一个边任务,对应辅助图中连续的两个相关点的遍历, 其中第一个点表示边服务的顺序。
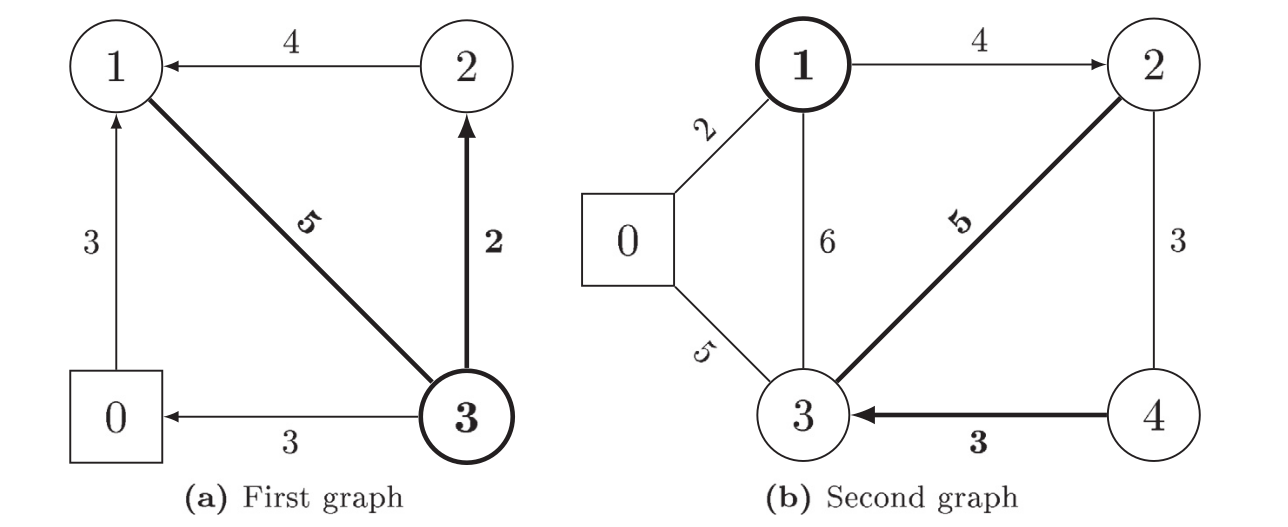
以figure. 1b为例,考虑原图上路径$[0,1,3,2,4,3,0]$,其中点$1$,边$(2,3)$,弧$(4,3)$
为服务,对应辅助图上的服务序列$[0_1,1,(3,2),(2,3),(4,3),0_2]$,整个的服务成本为$24$
作者其实在这里并没有讲清楚这么设计的理由,为此做一下说明, 一个很朴素的想法是将边任务分解为两个点,每个点表示一种服务方式,但基于这种方式 构建的辅助图并不能保证连通性,这两个分解点之间是不连通的。 为此在要保证辅助图连通性的要求下,对分解出的两个点之间的关系进行建模, 这也是为什么文中采用了上述看起来比较奇怪的方式建模。
2.2.2 travel time的转化建模
travel time的建模方式与cost的建模方式是一致的,这里就不做过多的赘述, 但这里需要注意的是,在辅助图的场景下,相应点的时间窗大小需要做调整, 核心思路是在辅助图上的遍历过程所产生的相关信息能够与原图上的遍历过程匹配
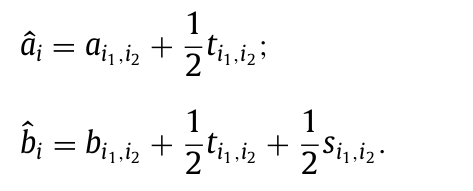
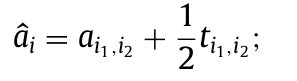
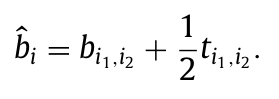
这里作者并没有讲清楚时间窗的转换思路,为此这里需要进一步阐述一下
-
对于弧任务,在辅助图的场景下,抵达相应点在原图上等价于抵达这条弧的中点, 所以需要加上相应的偏移$\frac{1}{2}t_{i1,i2}$
-
对于边任务,我们知道在辅助图的场景下,需要保证两个点连续的访问,这里就存在两种情况
- 该点是其中的第一个点,这种情况与弧任务的情况一致,偏移为$\frac{1}{2}t_{i1,i2}$
- 该点是其中的第二个点,这时前面已经访问过其反向对应的点,此时的偏移需要加入上一个点的 服务时间,总偏移为$\frac{1}{2}t_{i1,i2}+\frac{1}{2}s_{i1,i2}$
为此整个时间窗的的最大可行区间就是第一种情况与第二种情况的所构成的大区间
3. 求解思路
这里作者使用了整数规划的技术来求解问题,这一部分并不是很熟悉,所以暂时不阐述, 待以后补充
4. 算例说明
文章使用了三类测试算例
- BHW, 大规模MCGRP算例
- CARPTW,有时间窗约束的CARP算例
- MCGRPTW,基于前两类算例生成
具体的生成规则在文章中有介绍,生成规则比较简单,这里就不赘述。 第2类和第3类测试算例作者并没有公开,如果有需要,可以邮件联系作者
5. 文章思考
- 本文的结合考虑了混合车辆问题以及时间窗问题,通过辅助图的设计,
将原问题转变为了VRPTW问题,使用整数规划的技术来求解
- 本文是MCGRPTW的第一篇文章,并且使用的是精确算法求解,在大规模问题上仍有较大的提升空间
-
Exact methods based on node-routing formulations for undirected arc-routing problems. Networks, 47 (1), 52–60 . ↩