1. 最短路径算法所基于的假设
- 图中的边权值非负
- 图中存在权值为负的边,但不构成负环
- 图中存在权值为负的边,并且构成负环
针对不同的假设,算法的适用性也会不同
2. Floyd-Warshall算法
该算法基于动态规划的思想,其中定义状态函数$f[k][i][j]$, 表示从$i$到$j$在只能经过前$k$个点的约束下,最短的路径长度。 \[f[k][i][j] = \min(f[k-1][i][j],\quad f[k-1][i][k]+f[k-1][k][j]) \tag{1} \label{1}\]
\eqref{1}式表示要么不使用第$k$个点做中继节点,要么使用第$k$个节点做中继节点。
- 可以用来求解任意两个点之间的最短路径
- 可以检测出位于负环内的点,但无法检测出不在负环内,但可达负环的点
- 可以解决存在负边的情况
- 空间复杂度$O(n^2)$,时间复杂度$O(n^3)$
2.1 滚动数组优化
由\eqref{1}式可以看出第$k$层的状态只取决于第$k-1$层的状态, 为此可以考虑使用滚动数组的方式来优化空间复杂度
考虑在滚动更新过程中,$f[i][j]$完成更新后,对$f[m][n]$进行更新 \[f[m][n] = \min(f[m][n],\quad f[m][k]+f[k][n])\]
如果$\{m=i,k=j\}$或者$\{n=j,k=i\}$,这时更新完成后的$f[i][j]$会参与到 更新过程中。因为这时$j=k$或$i=k$,则$f[i][j]=f[i][j]+f[j][j]$或 $f[i][j]=f[i][i]+f[i][j]$,这时更新后的数值与更新前的数值比并没有变化, 所以并不会影响求解的过程。
2.2 路径信息的计算
定义$path[i][j]$表示从点$i$到$j$所经过的节点k,那么就可以用递归的方式求得 最短的路径信息
假设$path[i][j]=k$,那么从$i$到$j$的最短路径就可以用如下递归表达式表示 \[i \rightarrow path[i][k] \rightarrow k \rightarrow path[k][j] \rightarrow j\]
3. Dijkstra算法
基于贪心的思想,用于求解单源最短路径的问题,只能用于求解非负数边的情况
- 不能处理负权边与负权环的情况
3.1 基本算法
维护以下数据结构:
- $A$: 已经确定的源点到该点有最短路径的点的集合
- $B$: 还未确定的源点到该点有最短路径的点的集合
- $d_i$: 目前源点到$i$点的最短路径值
迭代执行以下两个过程:
- 选择阶段,执行$\mathop {arg\min} \limits_{i}d_i, i \in B$, 将对应的$i$加入$A$
- 松弛阶段, 执行$d_j=\min \{ d_j, d_i+ cost_{ij} \}, j \in B$
因为非负边的假设,所以可以保证在选择阶段确定的点之后一定不会被松弛, 从而保证了算法的正确性。但在负边存在的情况下, 即使在选择阶段当前是最小距离,在后续的松弛操作时,因为负边的存在, 仍有可能被进一步松弛,从而导致了算法的失效。 (考虑下图以$A$点为源点的计算过程)
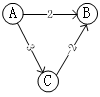
3.2 复杂度优化
可以看出Dijkstra的复杂度为$O(n^2)$,如果计算全图所有的点,则为$O(n^3)$, 在内层循环中,需要找出$B$集合中最短距离点$i$, 可应通过优先队列的结构来将相关操作复杂度优化为$O(\lg n)$ 这样整个算法的复杂度会变为$O((E+n)\lg n)$,当图为完全图时, $E=\frac{n(n-1)}{2}$, 退化为$O(n^2\lg n)$
4. Bellman-Ford算法
用于解决单源最短路问题,相比于dijkstra算法,通用性更强,但复杂度更大。
- 对边的情况没有要求,可以处理负边与负环的情况
4.1 算法思想
通过边集对整个距离矩不断阵进行松弛操作,来求得最短路径,复杂度为$O(NE)$ \[d_j=\min(d_j,d_i+cost(i,j))\]
假设从源点到点$a$的最短距离由$k$条边构成,那么我们可以保证在第$k$轮松弛后,
从源点到$a$点的最短路径可以被找到。
证明: 考虑从点$v$到点$a$存在一条最短路径,$(p_0=v,p_1,…,p_k=a)$,
在第一轮松弛前,我们可以保证到点$p_0=v$的最短路径已经被找到,
在第一轮松弛的过程中,可以肯定边$(p_0,p_1)$参与到$p_1$的松弛过程中,
从而确保在第一轮松弛后,到点$p_1$的最短路径被确定。重复上述过程,
可以保证在$k$步之后,找到到$a$点的最短路径。
4.2 路径构建
维护$predecessor$数组,$predecessor[i]$表示从源点到$i$点 的最短路径中的倒数第二个点。如果用边$(u,v)$可以松弛点$v$, 那么$v$点的 前驱节点更新为点$u$.
4.3 负环的判断
如果在第$|N|$次图仍可以被成功松弛,那么说明图中存在负环
5. SPFA算法
SPFA算法是对Bellman-Ford算法的优化,在Bellman算法中,每一轮的松弛操作是对所有边遍历: 实际考虑如下松弛过程:
- 第一次松弛,能够松弛成功的边必定是与源点$s$邻接点相连的边
- 第二次松弛,能够松弛成功的边必定是上一步松弛的时候的邻接点与它们的邻接点相连的边
- …
考虑上述过程,我们可以对每轮松弛操作的搜索空间进行剪枝, 可以利用一个队列来记录每轮松弛所需要的搜索空间,类似BFS操作。
在构建搜索队列的时候,重复点不需要重复入队,因为重复点所生成的搜索空间是相同的