Bert 论文阅读
BERT (Bidirectional Encoder Representations from Transformers) 是在 2018年由google的Jacob Devlin等人提出的一个新的预训练语言模型。
预训练语言模型可以做什么
目前预训练模型在NLP中主要有两种应用策略
-
feature-based: 使用预训练模型的词向量作为下游任务的输入特征, 其中的代表是ELMo(2018)。
-
fine-tuning: 将上游预训练模型与下游任务进行统一的训练,其中的代表是Open AI GPT(2018) , BERT(2018)。
总的来说,个人感觉两类方式的主要区别就是是否在下游任务中对预训练模型的参数进行微调。
为什么提出BERT
之前的预训练模型架构诸如ELMo,GPT都使用了单向的语言建模模型
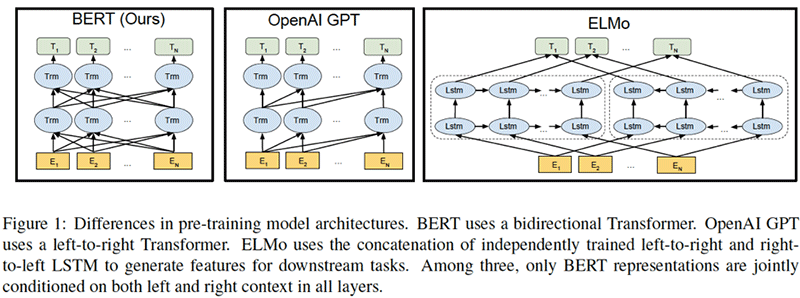
| 模型 | 特点 | 问题 |
|---|---|---|
| ELMo | 双向LSTM架构 | 串行encode,无法并行 |
| GPT | left-to-right 架构,每个token只能利用到它之前的信息 | 在需要下文信息的任务上,如QA表现较差 |
BERT的目标就是解决上述两种模型所面对的问题
- 支持并行解码
- 利用到上下文信息
BERT如何做
1. 建模思路
\[\mathop{\arg\max}\limits_{\theta}\prod_{t=1}^{T}P_{\theta}(\overline{x}|\widehat{x})\]$T$指整个序列长度,$\overline{x}$表示当前序列中被mask的单词, $\widehat{x}$指的是当前序列中没有被mask的单词,整个建模的思路很简单,就是求 基于当前未被mask的所有单词,使得被mask的单词的似然度接近ground truth。
对目标函数对数化,可以得到 \[\underset{\theta}{\max}\sum_{t=1}^{T}\log P_{\theta}(x_t|x_{< t}) =\sum_{t=1}^{T}\log\frac{\exp (h_{\theta} (x_{1:t-1})^{T}\cdot e(x_{t}))}{ \underset{x' \in vocab}{\sum}\exp (h_{\theta}(x_{1:t-1})^{T}\cdot e(x'))}\]
2. 模型结构
使用Transformer(2017)的Encoder架构来支持基于上下文的并行编码
- 输入特征构建
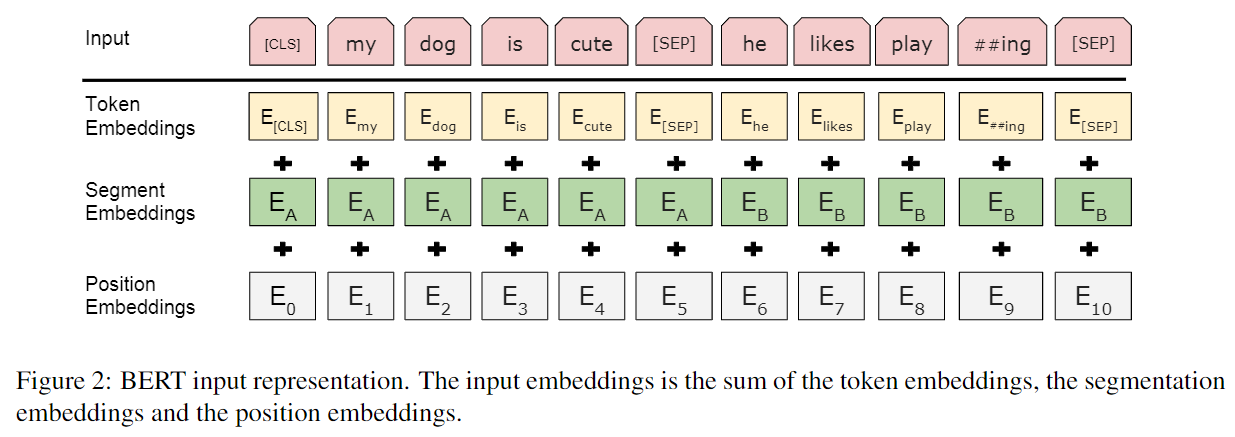
- WordPiece embeddings分词(2016),获得token embedding
- Segment embeddings, 用来区分不同的句子
- Position embeddings, 512个
上述的输入向量均是可训练的。
一些特殊的符号
- CLS,special classification embedding,用于对输入序列的整体进行编码
-
SEP,输入多个句子时,用于区别不同句子
- 模型规格
| 模型 | layer | hidden state size | attention head | 总参数量 |
|---|---|---|---|---|
| BERTbase(与GPT规模相同) | 12 | 768 | 12 | 110M |
| BERTlarge(最优结构) | 24 | 1024 | 16 | 340M |
2. 训练方式
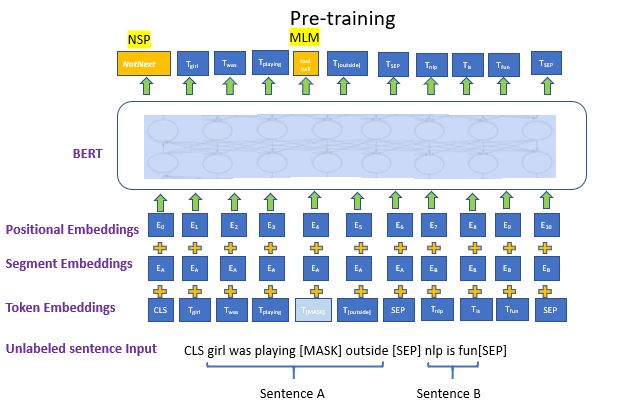
使用无标注的预料数据来进行半监督学习,主要训练策略有两种
-
使用 MLM(maksed language model)训练方式,这种方式受完 形填空的启发(Cloze task,1953),通过随机mask(15%)输入中的若干 token,让模型去预测被mask的token,这种方式同时利用了上下文的信息, 解决了GPT的缺点。
-
使用NSP(next sentence prediction),以50%的概率选择连续上下文 句子对,以50%的概率选择非连续的上下文句子对,让模型去预测句子对是否 匹配。
但是存在以下问题:
mask并没有出现在下游任务中,会导致上下游的不一致性,解决方法就是通过 对mask策略加入一定扰动,这样模型不知道要预测哪个token,从而减轻这种 不一致性带来的问题。
| 概率 | 方法 |
|---|---|
| 80% | 替换为mask |
| 10% | 替换为其他token |
| 10% | 保留原token |
此外,在XLNet(2019),使用了一种全排列的训练方式, 从而避免了MLM方法内生的问题。
3. 激活函数
在神经网络的建模过程中, 模型很重要的性质就是非线性(如各种sigmoid,RELU激活函数),
同时为了模型泛化能力,需要加入随机正则(如dropout,随机置一些输出为0, 其实也是一种变相的随机非线性激活)。
而随机正则与非线性激活是分开的两个事情, 而其实模型的 输入是由非线性激活与随机正则两者共同决定的。
在激活函数中,sigmoid容易梯度消失,Elus与Relu缺乏随机因素(非零输出是固定的)。
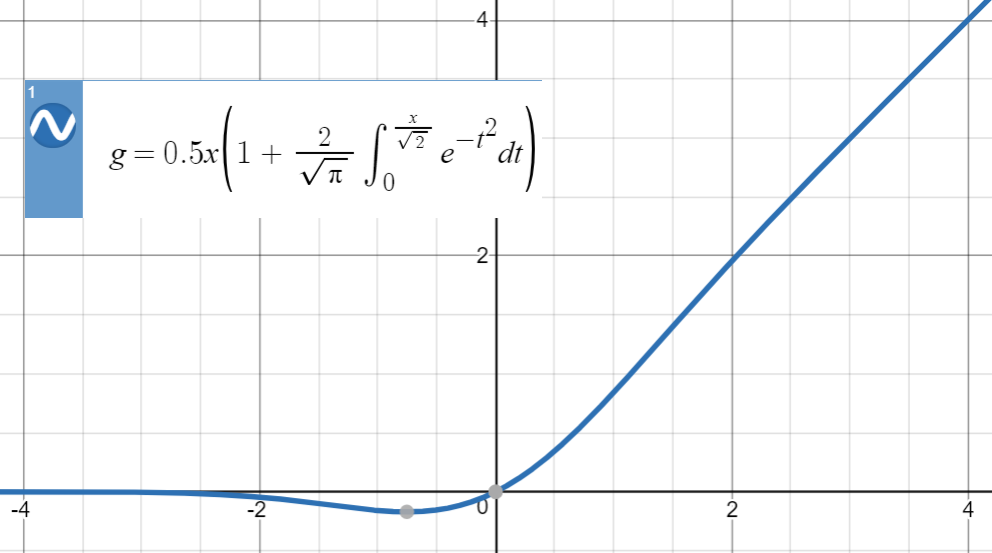
GELUs正是在激活中引入了随机正则的思想,将两者进行了结合 \[GELU(x)= xP(X\leqslant x)=x\Phi (x)\]
GELUs对于输入乘以一个取值范围为[0,1]的mask,而该mask的生成则是依概率随机的依赖于输入。 假设输入为X, mask为m,则m服从一个伯努利分布($\Phi (x),\Phi (x)=xP(X\leqslant x)$,X服从标准正太分布)。
这么选择是因为神经元的输入趋向于正太分布,这么设定使得当输入x减小的时候,输入会有一个更高的概率被dropout掉, 这样的激活变换就会随机依赖于输入了。一句话总结,随着 x 的降低,它被归零的概率会升高。
一般在实作时,会采用如下的近似函数 \[GELU(x)=0.5x(1+\tanh [\sqrt{\frac{2}{\pi}}(x+0.044715x^{3})])\]