文章参数说明

05/09/2020 #vrp

1 算法类别

1.1 全局参数

参数名	说明	默认值
phase number	搜索执行次数，一次执行表示一次完整的搜索, 如果为-1,表示会一直执行	1
random seed	随机数种子	0
search_time	搜索时间(秒)	60

1.2 邻域搜索

参数名	说明	默认值
neighbor search mode	邻域搜索模式 1. RTRIDP 2. IDPRTR 3. 随机	random
neighbor size	邻域表达小	25
significant search	在一次可行下降搜索中，如果实际move次数小于该阈值，则结束可行下降搜索	5
local ratio	在一次可行下降搜索中，如果没有导致成本变化的move占总move的比重超过该阈值，则结束可行下降搜索	0.8
max RTR search cycle	随机禁忌下降搜索过程中，最大允许搜索次数，该参数的作用类似与number of children	50
local minimum threshold	在邻域搜索中，判断是否到达局部最优点	40
tabu step	在劣解可行搜索过程中，禁忌步数	500
infeasible distance	在非可行邻域搜索中，当前解距离可行区域的距离阈值，大于为过远，反之为过近	0.3

1.3 种群搜索

参数名	说明	默认值
evolve steps	种群搜索总进化次数	5
pool size	种群大小	5
QNDF weights	种群解中解质量-距离参数	0.6

在种群搜索中，解的fitness由如下计算: $f(s)=QNDF \ast cost(s) + (1-QNDF) \ast mean(dist(s,{s}’))$

2 算法的策略细节

2.1 搜索策略

2.1.1 RTR搜索

在可行空间内的搜索策略

local_minimum_likelihood = 1, 局部最小值似然度
local_threshold, 局部最小值阈值
cnt, 搜索尝试次数
max_RTR_search_cycle, 最大搜索尝试次数

do{
    orig_val_for_uphill = 阈值禁忌搜索()
    
    do{
        cur_solution_cost = 下降搜索()
    }while(cur_solution_cost<orig_val_for_uphill)
    
    if(cur_solution_cost < orig_val_for_uphill){
        local_minimum_likelihood++
        cnt++
        if (cnt == max_RTR_search_cycle):
            local_minimum_likelihood = local_threshold
    }        
    else{
        local_minimum_likelihood += 1
    }    
    
}while(local_minimum_likelihood < local_threshold)

2.1.2 IDP搜索

在非可行空间内的搜索策略

在本阶段目标函数变为了 \[\begin{eqnarray*} f(x)&=&cost(x)+\beta\ast \sum_{r_i \in R}\max(0,load(r_i-C)) \\ \beta&=&\frac{cost(\bar{x})}{C\ast15} \end{eqnarray*}\]

$\bar{x}$表示当前已知可行解，解的搜索起点为当前已知最优解

初始化beta参数

小步非可行下降搜索()
小步非可行禁忌搜索()
if(当前解非可行){
    修复当前解()
}

	小步非可行下降搜索	小步非可行禁忌搜索
move operator	single insert，double insert, 2-opt, swap	single insert，double insert, 2-opt, swap
解接受策略	BEST ACCEPT	BEST ACCEPT
beta参数调整	是	否
是否多轮循环	是	否
固定neighbor size	是	是

2.2 Local Search

move operator:

invert
single insert
double insert
2-opt
swap

move 操作实现是通过rebuild的思想来实现的

Local Search move

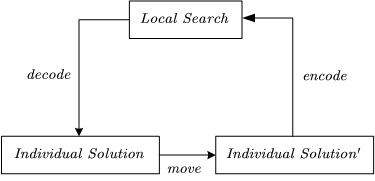
2.3 High speed Local Search

move 操作实现是通过dynamic programming的思想来实现的。

2.3.1 move operator:

invert
single insert
double insert
2-opt
swap
extraction
slice

前5种扰动都属于任务级别的扰动，为了增加邻域多样性，设计了后两种路径级别的扰动

2.3.2 采用分层解信息构建设计

底层是完整解信息的表示，借鉴LRU cache设计思想，通过双向链表+Hash数组来实现$O(1)$复杂度的搜索。此外为了为了更好地对路径信息进行建模，在路径之间插入Dummy Node,借鉴内存池的想法，对Dummy Nodes进行动态管理，减少内存的申请释放的开销。
上层为路径信息层，是对底层信息的聚合，包含路径的ID，起始点，载重，长度，服务数等元信息，该数据结构用于move的预判断，同样路径信息也属于动态资源，使用资源池的设计进一步减少系统级的内存调用。

在执行move操作的时候，两层信息的同步处理均可以在$O(1)$的时间复杂度内完成

High Speed Local Search move

2.4 move operator设计

2.4.1 single insert

将一个任务插到另一个任务的附近(前面或后面)

当待插入点是Dummy Node时，需要遍历每一条路径的起点与终点，并尝试插入其附近的位置
当待插入点不是Dummy Node时，需要考虑两个任务是否相邻
- 如果不相邻，需要同时考虑前插和后插两个位置
- 如果相邻，则是能考虑插入一个位置

2.4.2 double insert

将连续的两个任务插入到另一个任务的附近，连续的任务是指在一条路径中连续服务的一组任务

当待插入点是Dummy Node时，需要遍历每一条路径的起点与终点，并尝试插入其附近的位置
当待插入点不是Dummy Node时，需要考虑待插入任务序列的端点与插入任务是否相邻
- 如果不相邻，需要同时考虑前插和后插两个位置
- 如果相邻，则是能考虑插入一个位置

在普通Local Search中，插入位置只考虑了后插入，在High Speed Local Search 中考虑了两个方向上的插入。
此外需要注意在插入前需要检查是否有overlap的情况，即插入任务包含在待插入序列内部

2.4.3 2-opt

对路径进行切割重连的操作

三种不同的情况

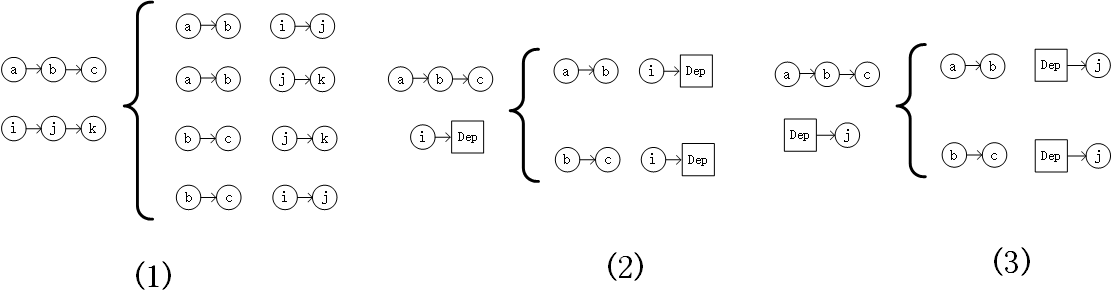
对于两个任务属于同一个路径，进行反转操作

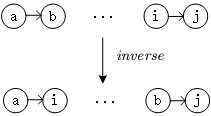flip
对于两个任务不属于同一个路径，进行cross over操作

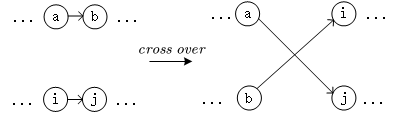cross over

2.4.4 Swap

交换两个任务的位置

当待插入点是Dummy Node时，需要遍历每一条路径的起点与终点，并尝试交换两者的位置
当待插入点不是Dummy Node时，直接交换两者的位置

2.4.5 Invert

反转任务，即反转一个边任务

2.4.6 Extraction

路径级别的扰动，将一个路径分割为三段子路径

2.4.7 Slice

路径级别的扰动，将一个路径切割为两段子路径

pre slice，切割点在备选任务前面
post slice，切割点在备选任务后面

因为涉及到路径的增加，上述两个operator只在阈值禁忌搜索的过程中会执行有效操作。此外上述两个算符属于单目算符，并不涉及到neighbor空间的搜索

3. 约束处理

3.1 载重约束

载重约束可以看作0维约束，给定一个服务序列$W=\{w_1,…w_n\}$，载重约束顺序无关，时间复杂度$O(n)$ \[Demand(i):\sum_{j=1}^{i}d(W_j)\leqslant C, \forall i \in W\]

3.2 时间窗约束

时间窗约束可以看做1维约束，给定一个服务序列$W=\{w_1,…w_n\}$，时间窗约束顺序相关，时间复杂度$O(n)$ \[a_{i} \leqslant DriveT(i):t_{depot,W_1}+\sum_{j=2}^{i}t_{W_{j-1},W_{j}} \ + \sum_{j=1}^{i-1}s_{W_{j}}\leqslant b_i, \forall i \in W\]